Math-Art T-Shirts

(October 2012) This shows 30 of the 120 dodecahedra of the 120-cell, one of the regular 4-dimensional polytopes radially and then stereographically projected from R⁴ to S³ to R³. This design is based on the solution to a puzzle that Saul Schleimer and I invented/discovered, and which is available from my shop at Shapeways.com.

(August 2012) This is an updated version of the design for the JuggleFest T-shirt. Rick Rubinstein did some touch ups on the front drawing, and rescanned. Unlike most of the other T-shirts here, these are pixel based rather than vector based images.

(January 2011) This design is made from concentric fractal curves, the outermost of which approach the Koch snowflake. This is the fourth step of the construction, starting from a hexagon. At each step of the construction, the number of curves doubles.

(January 2011) These fractal curves fill the "fudgeflake", a 3-rep-tile, meaning that 3 of them can be put together to form a larger version of the same tile (in the case of the fudgeflake, rotated 30 degrees). On the back of the shirt (the second image here) is the 6^th step of the fractal construction, while on the front are 3 copies of the 5^th step, fitting together to show how the fudgeflake tiles.

(December 2010) On the front and back are the two Kinoshita-Terasaka mutant knots, which are related to each other by a mutation move, which here turns over the kidney shaped tangle on the left. The two knots are difficult to distinguish, as they have the same hyperbolic volume and the same HOMFLY polynomial.

(December 2010) A stage in the construction of a space filling curve based on the pinwheel tiling. Space filling curves, such as the Hilbert curve are most often based on nested square grids, but they can also be based on other rep-tilings, such as the pinwheel tiling.

(April 2010) These designs are based on the Hopf Fibration, stereographically projected from the standard embedding of S³ in R⁴ to R³. Also see the 3D model based on the same construction.

The fibers are shown by rectangular cross-section tubes, each edge of the tube is a fiber. Generated using rhino.Python scripts, Rhino and Illustrator.

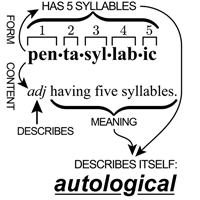
(March 2009) Updated version of the image I use to link to my page on Autological words.

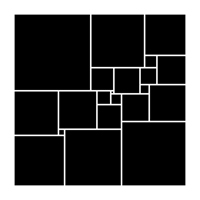
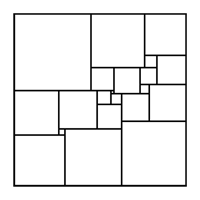
(Jan 2009) This is the smallest solution to the problem of taking a square and dissecting it into a number of smaller squares, such that all of the smaller squares are of different sizes, in the sense that it requires the fewest number of smaller squares, 21. It was discovered by A. J. W. Duijvestijn in 1978.

(July 2008) Third iteration of the Peano-Gosper space filling curve, with some extra added edges in the lower right to close off the path. From a Mathematica notebook with some editing in Illustrator.

(June 2008) The figure 8 knot, rendered in Rhino then traced in Illustrator.

(June 2008) Five tetrahedra arranged within a dodecahedron, also one of the stellations of the icosohedron. Designed in Rhino then imported into Illustrator.

(June 2008) Based on a spiral I've used elsewhere, generated and Voronoi diagramed in Mathematica. Colouring of nodes is based on the mod 2 and mod 3 values of the number of the node.

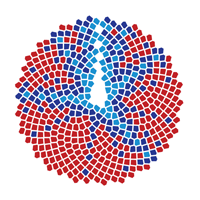
(June 2008) Another colouring scheme, this time using a "metric" on the natural numbers, based on how many Fibonacci numbers you need to add together to sum to the number. Here the white nodes are the Fibonacci numbers themselves, light blue is 2 Fibonacci numbers, dark blue 3 and red 4 or more.

(June 2008) A vector version of an autologlyph from 2002. Designed in Illustrator.

(June 2008) Another updated autologlyph. This version is a little cleaner in that it only goes up to pentominoes, and the polyominoes are at only 45 degree angles.

(September 2011) Not actually a T-shirt as far as I know, but this logo for the Stanford Mathematics Research Center fits here. The design is in the same style as, but different from the design I made for the Stanford Mathematics Department.

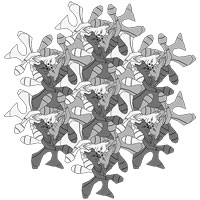
(January 2010) A design for the Texas Juggling Society's Jugglefest. I did the tessellation design (and the back of the T-shirt, the second image here) and then Rick Rubenstein (who did a degree in drawing before he became a professional juggler, but now works at Apple) took the tessellation and worked it into the front of the shirt (the first image here), based on Escher's Reptiles print. There was much discussion of the appropriately juggley replacements of the objects in the print.

My brother Will happened to have the right combination of waistcoat, bellbottoms and hair that can be fashioned into ears, in order to serve as a model for the cat.

The juggler is a cat because the need to define the shoulder led to ears, and the bellbottoms are needed to deal with other surrounding shapes of clubs. The waistcoat/suit jacket just seemed to fit.

(October 2009) Another University of Texas at Austin Math Club T-shirt. Based on a design by Neil Hoffman.

(October 2009) A repurposing of the figure 8 knot design for the Stanford University Math Department's T-shirt, in two different styles.

(March 2009) Design for the University of Texas at Austin Math Club's T-shirt. Texas fits together with itself remarkably well.