Second Life

(Dec 2008) Philips asked me to help with the roof of a recreation of "Poème électronique", a pavillion they made for the 1958 Brussels World's Fair, on their island Philips. The roof is made from a number of hyperbolic paraboloids that meet along straight lines.

(Oct 2008) "Rhombicosidodecahedron dual". Art Laxness designed the pieces, and I fitted them together to form this shape for a dome that Kim Anubis' company The Magicians made for a build for Wiley. The rhombicosidodecahedron is an Archimedean solid made from triangles, squares and pentagons. I replaced each polygon with a "star shape" of the appropriate number of points, and if we also straightened out the bends between stars we would get the dual polyhedron, the deltoidal hexecontahedron.

There are lots of interesting symmetries, with 2, 3 and 5 fold rotations.

(Aug 2008) "Noobility". This was a large project I did with my brother Will Segerman (Art Laxness in Second Life) for Rezzable's Black Swan sim. It involves fake avatars, the golden ratio, deadly traps, procedural generation, creation and destruction, all cycling once an hour. Bettina Tizzy has a comprehensive write-up.

(Jan 2008) "Fractal Tree". This comes from an idea suggested by Scope Cleaver. More experiments with sculpties to get the most out of the prims. This one is good for seeing visually the limit of a geometric series.

(Dec 2007) This is a geodesic dome, built with scripts. The biggest triangular face is just under the 10m size limit for ordinary prims, and the base is made from a single mega-prim.

(Dec 2007) "Hilbert Cube". Made out of 16 sculpty prims, which use the RBG values on a texture to define the XYZ positions of vertices in a mesh. I generate sculpty textures using various python programs. This shows a few iterations of a 3 dimensional analogue of Hilbert's space filling curve.

(Aug 2007) "Fibonacci Pinecone". This was a prototype for a book cover, details are here. The scripts used were modifications of the ones I used for "Spore".

(Apr 2007) "Split Torus". This can be seen as an ordinary torus, cut and opened up, except that which is (was?) the inside of the torus and which is the outside is ambiguous: the two sides are identical.

(Jan 2007) "Lorenz Attractor". This is a dynamic sculpture: the white ball follows the equations of the Lorenz system (or rather, it makes discrete jumps approximating them), and lays prims showing the path it takes behind it. Also see: Youtube video.

(Dec 2006) "Archimedean Spire". This is a ruled surface, that is a surface made up of straight lines. The ends at the base of the sculpture follow an Archimedean spiral, the other ends just move up the spire at a constant rate.

(Dec 2006) "Spore". This is based on a process that turns up in nature a lot: 'growing' new objects around some axis at an angle of 2pi/Phi from the previous one, where Phi is the golden ratio, (1+sqrt(5))/2.

(Aug 2006) "Tetrahedron Man". This was my build for Burning Life 2006. The pattern of tetrahedra (with octahedra, filling space) was used by Escher in his "Flatworms" print, and I use it here to build a very large figurative sculpture.

(Aug 2006) "Figure 8 Knot Embedding 3". This is a particularly symmetric way to embed the figure 8 knot into space.

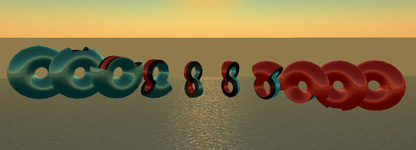
(Jul 2006) "How To Turn A Torus Inside Out". A punctured torus can be flipped inside out by a sequence of moves as shown.

(Jun 2006) A recreation of the house from Robert A. Heinlein's short story "--And He Built A Crooked House". See Hamlet Au's blog entry for an excellent write-up. Hamlet's story got picked up by BoingBoing, Digg et al, and was all over the internet for a couple of days. This slurl should take you to a teleporter to the house.

(May 2006) "Faces". This is a similar idea to the classic vase illusion.

(Apr 2006) This is a model of the Hopf Fibration, which is a remarkable way to define "flow lines" in 3 dimensional space. The Hopf Fibration gives the first known example of a non-trivial nth homotopy group of the m dimensional sphere with n greater than m, which was very surprising at the time.

(Mar 2006) The hypercube is the 4-dimensional analog of the cube. It has 16 corners, 32 edges, 24 square faces and 8 cubic cells. If you take two copies of a square, and join corners on one square to corners on the other with lines, you get a cube. In the same way, if you take two copies of a cube and join corners of one cube to corners of the other with lines, you get a hypercube.

This sculpture is a projection of the hypercube from 4d to the 3d of Second Life, just as the 3d of Second Life projects to the 2d of a computer screen. Just as on a screen, things that are further away appear smaller. Sometimes one can see a smaller cyan cube inside a larger red cube - the two cubes are the same size in 4d, but the cyan one is further away from us so it looks smaller. Distance from us is also indicated by the colour, and the thickness of the lines.

This is a "meandering" hypercube because (if it is running) it makes a small random 4d rotation every few seconds. One can touch the base to turn the rotations on or off. If one watches long enough one will be able to see how the hypercube's appearance changes as it rotates around.

This was essentially a scripting challenge, using the rotation data type in ways that it wasn't designed for!

(Mar 2006) The Costa-Hoffman-Meeks Surface is an example of a "minimal" surface, which are of interest to differential geometers. This version is a model of the rough shape, an approximation to the true shape to make it possible to build with the techniques I developed to make The Grail.

(Feb 2006) The Grail is as much a sculpture as a building, and was not designed with any particular purpose in mind, although it does have a fully functional "elevator" system involving avatar pushes. I had thought for a couple of months about how to build a large structure with no sharp corners (only smooth curves) and no seams. The Grail is one solution to that problem, combining a number of torus shape "discoveries", all worked out using algebra.

(Sep 2005) "Negative Curvature Fractal 4", another procedurally generated fractal. It has "negative curvature" in the sense that each piece is the inside curve of a torus, which has negative curvature. If it were possible to fit those pieces together smoothly then the entire surface would have negative curvature. As it is there are some angles, but it retains some features of negatively curved surfaces: it gets very crinkly as one moves out towards the edges of it.

(Sep 2005) Graph of the surface given by the function z = xy, which like the hyperboloid can be made from straight lines.

(Sept 2005) Various views of my build for "Burning Life" 2005, Second Life's version of Burning Man. Lots of fractals, all procedurally generated, including an animated, randomly evolving one.

(Aug 2005) I wrote a set of scripts to automatically generate a fractal from a base primitive (shape) and copies of it. The base is red, the 'child' prims are green, and the generated fractal is next to it.

Also in one of the images here a hyperboloid, made out of straight lines. It is animated to rotate the lines around to get different hyperboloids.

(Aug 2005) Rhombic dodecahedra can, somewhat surprisingly, fill space. That is, you can stack them together to completely fill up 3d space. They are also closely related to diamond structure, as demonstrated here.

Squashed rhombic dodecahedra are better proportioned for people sized rooms, but the standard scale could also be useful.

(June 2005) A couple of torus knots and a diamond structure, in the sculpture garden in Montmartre (now long since derezzed).

(July 2005) An ordinary looking room one might think, until you see it from above. This is an Ames room, a kind of optical illusion.

People of similar heights standing in the two far corners of the room from the viewing window appear to be of very different sizes.

(July 2005) A classic illusion. When you click on the sign, the pieces rearrange themselves, and somehow an extra square appears!

(July 2005) A fractal sculpture, of an Alexander horned sphere.

(July 2005) More fractal sculptures, this time of wild knots. Three variations on the theme.

(July 2005) One sort of spiral. The math involved in getting this to work was nasty.

(July 2005) Another sort of spiral. This one was much easier to deal with.

(July 2005) This doesn't look that hard to make, unless you know that the maximum twist that Second Life allows in going around a single torus is 720 degrees. To get what looks like a single torus with a twist of 7,200 degrees involves parts of 20 tori.

(July 2005) A Sierpinski tetrahedron, made up of 256 small tetrahedra. It's fun to fly around inside of.

The second image is 4 of the previous ones, stacked together, to make an even bigger one, made up of 1024 small tetrahedra.